Ekstra eksempel til VA Miljøblad nr. 79.
Dimensjonering av avløpsledninger. Selvrensing.
En spillvannsledning i et separatsystem har innvendig diameter 300 mm. Den har tilførsel av spillvann fra 8000 personenheter og gjennomsnittlig spesifikk avløpsmengde er 250 l/p d.
Minimal døgnfaktor fmin er 0,8. Fallet på strekningen som skal sjekkes for skjærspenning er 8 ‰. Friksjonskoeffisienten er 0,018. Er denne ledningen selvrensende?
1) Anbefalt minimumsverdi for skjærspenning ( τmin) for spillvannsledning er 2 N/m2.
2) Neste trinn er å finne vannføringen i ledningen når den går helt fylt (Qfull). Darcy Weisbachs ligning for vannføringen i røret når dette er fylt er:
h = f (1)
h = falltap over hele rørets lengde (m)
f = friksjonskoeffisienten
L = lengde på røret (m)
D = diameter (m)
v = midlere vannhastighet i røret ved fylt rør (m/s)
g = gravitasjonen 9,81 i m/s2
Man kan nå beregne vannhastigheten v ved å omforme ligning (1).
v = (2)
Ved 8 ‰ fall vil en strekning på L = 1000 meter ha et fall og falltap lik h = 8 m.
v = = 1,62 m/s Vannføringen (m3/s) i det fylte røret blir ifølge kontinuitetsligningen:
Qfylt = v A = v π r2 = 1,62 ∙ 3,14 (0,3/2) (0,3/2) = 0,114 m3/s (3)
A = tverrsnittsarealet innvendig i røret (m2)
- Dimensjonerende vannføring for selvrensningsberegningen (Qdimselvrens)
Qdimselvrens = α ∙ P ∙ q ∙ fmin (4)
Qdimselvrens = dimensjonerende vannføring for selvrensningsberegningen
P = antall personekvivalenter
q = midlere spesifikt vannforbruk per personekvivalent og døgn (m3/P d)
fmin = minimal døgnfaktor (vannforbruk i årets minst forbrukende døgn dividert på midlere døgnforbruk) α = 1 + for P < 3000 personekvivalenter, og (5)
α = 1,43 for P > 3000 personekvivalenter (6)
Her blir α = 1,43. Med de viste α-verdier skal man være sikret en vannføring som varer minst 10 % av døgnet i alle døgn i året.
Qdimselvrens = α ∙ P ∙ q ∙ fmin = 1,43 ∙ 8000 ∙ 0,25 ∙ 0,8 = 2288 m3/døgn = 0,0265 m3/s
- Delfyllingen (h) i avløpsrøret ved dimensjonerende selvrensingsvannføring.
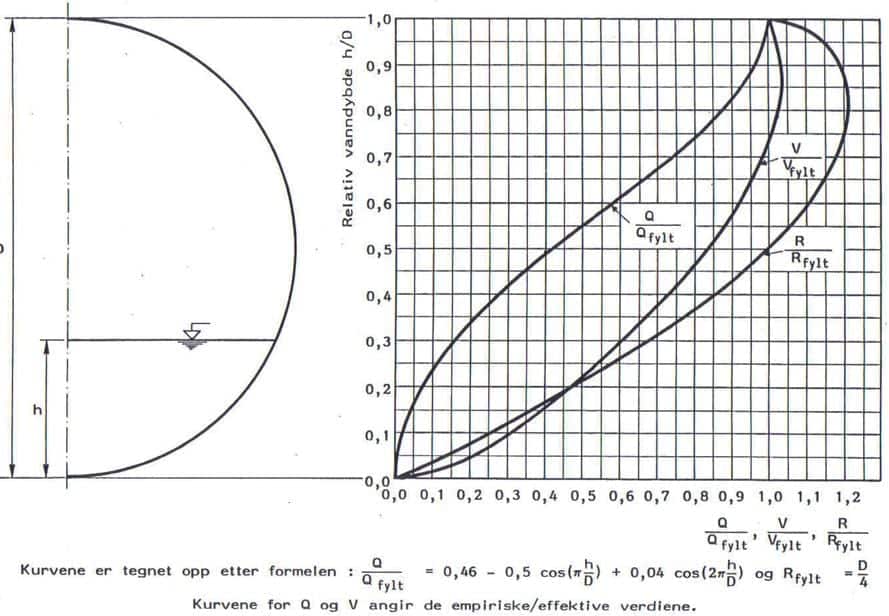
Delfyllingsdiagrammet under brukes når man vet forholdet mellom Qdimselvrens og Qfylt. Dette har man nå beregnet i punkt 2 og 3. Man går inn med Qdim/Qfylt på horisontalaksen opp til øvre kurve, så til venstre mot aksen og finner relativ fyllingshøyde h/D.
Qdimselvrens / Qfylt = 0,0265 / 0,114 = 0,23
Av diagrammet finner man da at h/D = ca. 0,36
- Skjærspenningen (τfylt )ved fylt rør.
Skjærspenningen (N/m2) langs rørveggen i et sirkulært fylt rør er
τfylt = γ R I (7)
γ = vannets spesifikke vekt som kan settes til 10 000 N/m3
R = hydraulisk radius (m) = vått tverrsnittsareal/den fuktede randsonen i tverrsnittet.
For et fylt rør er hydraulisk radius R = π r2/ 2π r = r/2 = D/4
I = fall på ledningen i m/m. D.v.s. at 10 ‰ blir 0,01
τfylt = γ R I = 10 000 ∙ 0,3/4 ∙ 0,008 = 6 N/m2 6. Maksimal skjærspenning (τmaks ) i bunnen av røret ved Qdim.
Det er normalt ikke fylte rør i den kritiske situasjonen, men en mindre delfylling i rørene. Skjærspenningen er da null i vannoverflaten på rørveggen og økende til en maksimal verdi (τmaks) i bunnen av røret.
For en delfylling opp til h/D = 0,25 brukes følgende formel for τmaks
τmaks = τfylt 4 (1 – ) = 6 ∙ 4 ∙ 0,36 ∙ (1 – 0,36) = 5,53 (8)
- Sjekk om røret er selvrensende ved at τmaks er større enn τmin.
5,53 N/m2 er større enn kravet på 2 N/m2, så ledningen er derfor selvrensende.